|
A análise estatística do indicador é composta por cálculos auxiliares que permitem ter uma melhor visão dos valores do indicador. Esta análise é realizada pelo sistema no momento do cálculo do scorecard, e é possível visualizá-la nos detalhes do indicador ou na estrutura do scorecard, quando acessada pela tela de execução ou consulta, e se assim for definido no perfil de visualização aplicado a ele. Os cálculos que compõem a análise estatística são:
Trata-se de uma média simples das medições, que utiliza o período de acumulação para realizar o cálculo. Ou seja:
Ritmo = Média(Medição)
|
Para seu cálculo é necessário o acumulado das metas. O cálculo realizado será:
Ritmo faltante = (Acumulado meta - Acumulado medição) / Nr. meses faltantes
|
Para seu cálculo é utilizado o método dos mínimos quadrados. Este é o mesmo método utilizado pelo Excel para calcular a tendência. Por meio deste método é obtida uma reta dos mínimos quadrados que melhor ajuste entre os pontos desejados, bastando para isso, resolver o sistema linear com 2 equações e 2 incógnitas a1 e a0.
Tendência = a0 + a1*X
a0 = ((SY * SX2) - (SX * SXY)) / ((N * SX2) - (SX * SX))
a1* = ((N * SXY) - (SX * SY)) / ((N * SX2) - (SX * SX))
|
Sendo:
X = Número do período
Y = Valor da medição/realizado
N = Número de períodos utilizados
SX = x1 + x2+...+xN = Soma dos números de períodos utilizados
SY = y1 + y2+...+yN = Soma das medições (valor realizado) dos períodos utilizados
SXY = x1y1 + x2y2+...+xNyN = Soma dos produtos entre os períodos utilizados e as medições
SX2 = (x1)² + (x2)²+...+(xN)2 = Soma dos quadrados de períodos utilizados
|
*O coeficiente a1 determina a inclinação da reta.
|
Também conhecida como amplitude amostral (a) de um conjunto de n* valores x1, x2, ..., xn* é definida pela diferença entre o maior valor (xmax) e o menor valor (xmin) do conjunto, ou seja:
a = xmax - xmín
*n = parâmetro de períodos para análise de estatística do indicador
|
A variância (s2) de um conjunto de dados x1, x2, ..., xn* é a média aritmética dos quadrados dos desvios desses valores em relação à sua média aritmética, ou seja:
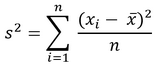
*n = parâmetro de períodos para análise de estatística do indicador
|
É definido como a raiz quadrada positiva da variância, ou seja:
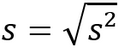
|
É expresso em porcentagem, sendo uma medida relativa de dispersão em relação ao seu valor médio. Trata-se de uma medida adimensional de dispersão, sendo definida como o coeficiente entre o desvio padrão (s) e a média aritmética, ou seja:
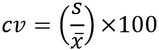
|
A média aritmética x de um conjunto de n* valores x1, x2, ..., xn, é definida por:
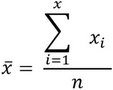
*n = parâmetro de períodos para análise de estatística do indicador
|
|







