|
El análisis estadístico del indicador es compuesto por cálculos auxiliares que permiten tener una mejor visión de los valores del indicador. Este análisis es realizado por el sistema al calcular el scorecard, y es posible visualizarlo en los detalles del indicador o en la estructura del scorecard, cuando se accede a través de la pantalla de ejecución o consulta, y si así es definido en el perfil de visualización que se le aplica. Los cálculos que componen el análisis estadístico son:
Se trata de un promedio simple de las mediciones, que utiliza el período de acumulación para realizar el cálculo. O sea:
Ritmo = Promedio(Medición)
|
Para su cálculo es necesario el acumulado de las metas. El cálculo realizado será:
Ritmo faltante = (Acumulado meta - Acumulado medición) / Núm. meses faltantes
|
Para su cálculo, se utiliza el método de los mínimos cuadrados. Este es el mismo método utilizado por Excel para calcular la tendencia. Por medio de este método, se obtiene una recta de los mínimos cuadrados que mejor se ajusten entre los puntos deseados, bastando para eso, resolver el sistema lineal con 2 ecuaciones y 2 incógnitas a1 y a0.
Tendencia = a0 + a1*X
a0 = ((SY * SX2) - (SX - SXY)) / ((N * SX2) - (SX * SX))
a1* = ((N * SXY) - (SX * SY)) / ((N * SX2) - (SX * SX))
|
Dónde:
X = Número del período
Y = Valor de la medición/realizado
N = Número de períodos utilizados
SX = x1 + x2+...+xN = Suma de los números de períodos utilizados
SY = y1 + y2+...+yN = Suma de las mediciones (valor realizado) de los períodos utilizados
SXY = x1y1 + x2y2+...+xNyN= Suma de los productos entre los períodos utilizados y las mediciones
SX2 = (x1)² + (x2)²+...+(xN)²2 = Suma de los cuadrados de períodos utilizados
|
*El coeficiente a1 determina la inclinación de la recta.
|
También conocida como amplitud de la muestra (a) de un conjunto de n* valores x1, x2, ..., xn* es definida por la diferencia entre el mayor valor (xmax) y el menor valor (xmin) del conjunto, o sea:
a = xmax - xmín
*n = parámetro de períodos para análisis de estadística del indicador
|
La varianza (s2) de un conjunto de datos x1, x2, ..., xn* es el promedio aritmético de los cuadrados de las desviaciones de esos valores con relación a su promedio aritmético, o sea:
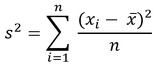
*n = parámetro de períodos para análisis de estadística del indicador
|
Se define como la raíz cuadrada positiva de la varianza, o sea:
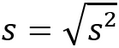
|
Se expresa en porcentaje, siendo una medida relativa de dispersión con relación a su valor medio. Se trata de una medida adimensional de dispersión, siendo definida como el coeficiente entre la desviación estándar (s) y el promedio aritmético, o sea:
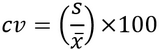
|
El promedio aritmético x de un conjunto de n* valores x1, x2, ..., xn, se define por:
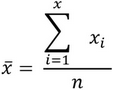
*n = parámetro de períodos para análisis de estadística del indicador
|
|







