|
The statistical analysis of the indicator is composed of auxiliary calculations that allow having a better view of the values of the indicator. This analysis is performed by the system at the time of calculating the scorecard and you can view it in the details of the indicator or in the structure of the scorecard, when accessed through the execution or view screen and if so is defined in the view profile applied to it. The calculations that comprise the statistical analysis are:
This is a simple measurement average, which uses the accumulation period to carry out the calculation. That is:
Rhythm = Average(Measurement)
|
For its calculation, it is necessary to accumulate the targets. The calculation performed will be:
Necessary rhythm = (Cumulative target - Cumulative measurement) / missing months #
|
For your calculation is used the method of the minimum squares. This is the same method used by Excel to calculate the trend. This method generates a line of the least squares which best fits between the desired points, thereby solving the linear system with two equations and two unknowns, a1 and a0.
Trend = a0 + a1*X
a0 = ((SY * SX2) - (SX * SXY)) / ((N * SX2) - (SX * SX))
a1* = ((N * SXY) - (SX * SY)) / ((N * SX2) - (SX * SX))
|
Where:
X = Period number
Y = Measurement/actual value
N = Number of periods used
SX = x1 + x2+...+xN = Sum of the number of periods used
SY = y1 + y2+...+yN = Sum of the measurements (actual value) of the periods used
SXY = x1y1 + x2y2+...+xNyN = Sum of the products between the used periods and the measurements
SX2 = (x1)² + (x2)²+...+(xN)2 = Sum of the squares of the periods used
|
*Coefficient a1 determines the line inclination.
|
Also known as sample range (a) of a set n* x1, x2, ... values, xn* is defined by the difference between the highest value (xmax) and the lowest value (xmin) of the set, that is:
a = xmax - xmin
*n = periods parameter for the indicator statistical analysis
|
The variance (s2) of a data set x1, x2, ..., xn* is the arithmetic mean of the squares of the deviations of these values in relation to their arithmetic mean, that is:
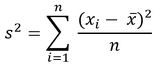
*n = periods parameter for the indicator statistical analysis
|
It is defined as the positive square root of the variance, i.e.:
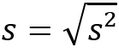
|
It is expressed as a percentage, a relative dispersal measure in relation to its average value. It is a dimensionless measurement of dispersion defined as the coefficient between the standard deviation (s) and the arithmetic mean, that is:
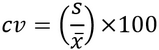
|
The arithmetic mean x of a set of n * values x1, x2, ..., xn, is defined by:
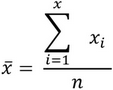
*n = periods parameter for the indicator statistical analysis
|
|







